モデル選択のためのペナルティ付きクロスバリデーション

※アーカイブの成果情報は、発表されてから年数が経っており、情報が古くなっております。
同一分野の研究については、なるべく新しい情報を検索ください。

要約

モデルを選択するための統計量として、クロスバリデーションにペナルティ項を加えたものを用いることによって、凸凹が多すぎる推定値を与えるモデルが選択されるのを防ぐ。ペナルティ項の大きさをデータに立脚して決める。

• キーワード: クロスバリデーション、モデル選択、ノンパラメトリック回帰、予測
• 担当:中央農研・農業情報研究部・生産支援システム開発チーム
• 連絡先:電話029-838-8975、電子メール takezawa@affrc.go.jp
• 区分:関東東海北陸農業・情報研究、共通基盤・情報研究
• 分類:科学・参考

背景・ねらい

各地で蓄積されたデータやモデルを総合的に利用して、信頼性の高い予測や制御を可能にするためには、様々な要素を加味した 複合的なモデルが必要になる。その際、従来のモデル選択基準を用いてモデル選択を行うと適切なモデルが得られないことが多くなる。そこで、クロスバリデー ションとクロスモデルバリデーションの関連に着目することによって得られる新しいモデル選択基準が必要になる。

成果の内容・特徴

• これまでモデル選択基準として広く利用されてきたクロスバリデーションに、モデルの複雑さに比例するペナルティ 項を加えたものをモデル選択基準として用いる方法を提案する。この方法を、pCV(penalized Cross-Validation, pCV=CV+α*c、cがモデルの複雑さを表す正の値 )と呼ぶ。pCVに対してペナルティ項を正の値にするという制約を加えたものがpCV+(penalized Cross-Validation plus、「+」は「プラス」と読む)である。いずれにおいても、ペナルティ項の比例定数をデータを用いて決定するので、データに適応的な(data adaptive)方法と言える。また、CMV(Cross Model Validation)とCMV+(Cross Model Validation plus)は、それぞれpCVとpCV+の前身と見なせる。
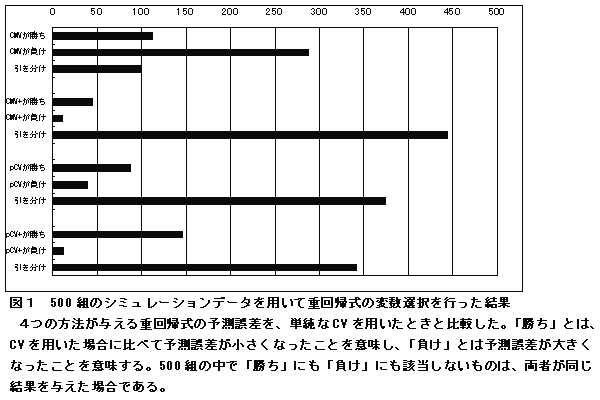
• これらの手法を比較するために、重回帰式の変数選択を行うためのプログラムをVisual Basic 6.0Jを用いて作製し、実行した結果が図1である。以下の式によるシミュレーションデータを用いている。
  yi = 2 + xi1 + 0.3xi2 + 0.03xi3 + 0.003xi4 + 0.0003 xi5 + ei
  ここで、xi1 、xi2、xi3、xi4 、xi5が予測変数で、0と1の間の値をとる一様乱数の実現値である。eiは、平均が0、標準偏差が0.1の正規分布の実現値である。それぞれのデータ数 は30個(1≦i≦30)で、疑似乱数の初期値を替えて作製した500組のシミュレーションデータを用いている。ここでの予測誤差とは以下のものである。
  30
  Σ( yi - ei - yi * )2/30 ( yi *はyi に対応する予測値)
  i=1
• 図1は、pCV+が最も優れた結果をもたらすことを示している。また、このシミュレーションに関する限り、CMVは優れた方法ではない。
• 多項式回帰において、CV、pCV、pCV+を比較した結果が、図2である。500組のシミュレーションデータのうち、真の値との差の2乗和が12未満のものの数は、CVでは409個、pCVでは416個、pCV+では426個である。pCV+が最も優れた結果を与えている。

成果の活用面・留意点

• pCV+とpCVは、複雑な回帰式におけるモデル選択においてより有効だと考えられる。
• pCV+あるいはpCVをそのまま用いると計算量が多くなりすぎることがあるので、クロスバリデーションの代わりに10群クロスバリデーションを使うなどの工夫が必要になる。

具体的データ

その他

• 研究課題名:データ・モデル協調型高精度生産支援システムの開発
• 課題ID:03-04-05-01-09-03
• 予算区分:交付金
• 研究期間:2003年度
• 研究担当者:竹澤邦夫
• 発表論文等:竹澤邦夫(2003) 応用統計学 Vol.32(1).31-42.