外れ値に対する重みを小さくすることよって回帰式の予測誤差を小さくする。

※アーカイブの成果情報は、発表されてから年数が経っており、情報が古くなっております。
同一分野の研究については、なるべく新しい情報を検索ください。

要約

外れ値と思われるデータを除くのではなく、重みを小さくすることで回帰式を作成すると予測誤差を小さくすることができる。外れ値の原因が不明で計算から除外することが適切か判断できない場合に有効。

• キーワード:重み付き回帰、ブートストラップ法、予測誤差
• 担当:中央農研・データマイニング研究チーム
• 代表連絡先:電話029-838-8948
• 区分:共通基盤・情報研究
• 分類:研究・普及

背景・ねらい

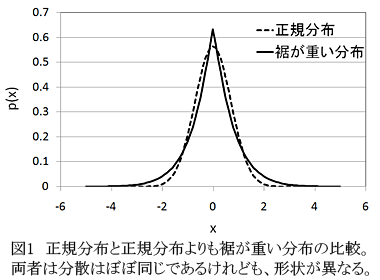
最小2乗法を用いて回帰式を作成するとき、推定値と実測値(データの目的変数の部分)の値が大きくずれているものがあることがある。それはしばしば外れ値として計算より除外される。どのデータを外れ値と見なすかは恣意的であることも少なくない。そこで、そのデータを除くのではなく、データに含まれる誤差が正規分布よりも裾が重い分布をしていて、外れ値は裾の部分に属していると想定する(図1)。これにより、外れ値と思われるデータには小さい重みを付けて回帰式を作る方法が導出され、与えられたデータを有効に利用した回帰式の実現が期待できる。この方法の有効性調べるために、ブートストラップ法(手元のデータのランダムサンプリングを行う方法)を利用して予測誤差を推定する。

成果の内容・特徴

• 本手法が想定する誤差の分布の様子を正規分布と比較したグラフが図1である。正規分布よりも裾が重い分布を仮定しているので、回帰式が与える推定値から大きく外れた実測値が生じるのは、当該データがこの裾の重い部分に属するためと考える。
• 手元のデータ全体から1つのデータを除いたものを用いて重回帰式を作成する作業を,除くデータを変えて繰り返すことによってそれぞれのデータに対する予測誤差を推定する。予測誤差(e_i)は以下のものになる。
  
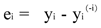
  ここで、{y_i }が実測値で、{y_i(^(-i))}がi番目のデータを除いたデータ用いて作成した重回帰式を用いてy_iに対応する推定値を求めた結果である。そして、i番目のデータに以下の重みを付け,全データで改めて重回帰を行い予測式を作成する。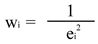
  
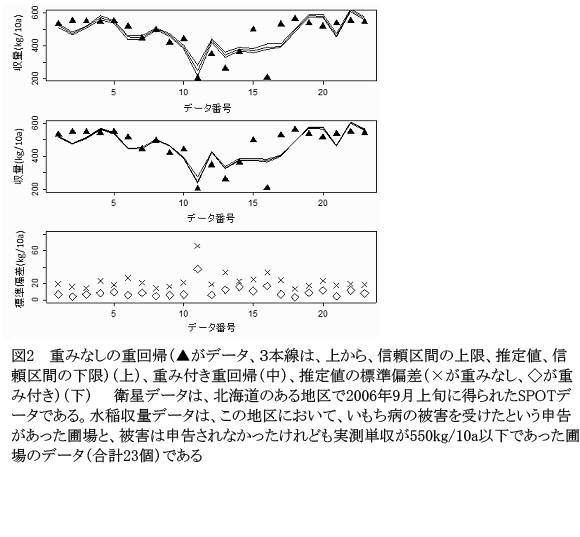
• ブートストラップ法を用いて、重みを付けずに得られた重回帰式による推定値と重みを付けて得られた重回帰式による推定値を比較し、得られた推定値の分散の大きさを調べる(図2)。重みを付けることによって、予測誤差が僅かに減少し、推定値の分散(ばらつき、信頼区間)は大きく減少する。また、これらのグラフによって、それぞれのデータの、推定値と予測値の関係や分散の大きさが分かり、個々のデータの由来に遡った検討に役立てることができる。
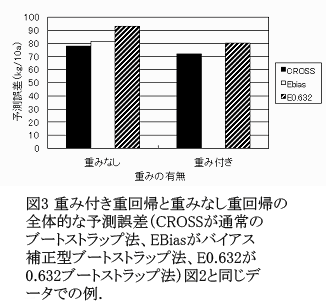
• 推定値の全体的な予測誤差の大きさを3通りのブートストラップ法を使って調べると、重みを付けたときの方が予測誤差が減少している(図3)。この予測誤差を得る際には重みを付けていないので、重み付き回帰によってデータ全体に対する予測誤差が減少することが分かる。

成果の活用面・留意点

• 外れ値の原因が不明で、除外することが適切か判断できない場合に利用できる。
• 重みを付ければいつも優れた結果が得られるとは限らず、本手法はさまざな回帰手法の1つとして試みるべきである。
• この手法を用いるためのRのプログラムの詳細については担当者に問い合わせる。

具体的データ

その他

• 研究課題名:多様かつ不斉一なデータの融合によるデータマイニング技術の開発
• 課題ID:222-c
• 予算区分:基盤研究費
• 研究期間:2006-2010年度
• 研究担当者:竹澤邦夫
• 発表論文等:システム農学 24(3)167-174.