自由度が整数でない回帰におけるF値を信用してはいけない

※アーカイブの成果情報は、発表されてから年数が経っており、情報が古くなっております。
同一分野の研究については、なるべく新しい情報を検索ください。

要約

直線回帰の結果とノンパラメトリック回帰の結果をF値を用いて比較するとき、ノンパラメトリック回帰に対応する自由度が整数ではないため、得られるF値は信頼できない。ブートストラップ法を用いた方法を利用すれば、この問題が克服できる。

キーワード:F検定、F値、直線回帰、直線性の検定、ノンパラメトリック回帰、ブートストラップ法
担当:中央農研・データマイニング研究チーム
代表連絡先:電話029-838-8948
区分:共通基盤・情報研究
分類:研究・参考

背景・ねらい

データを直線に回帰することが妥当かどうかを検定するとき、直線回帰の結果とノンパラメトリック回帰の結果をF値を用いて比較する方法が、多くの入門書で紹介されている。その際、ノンパラメトリック回帰における自由度は整数ではないため、得られるF値は近似的なものであることは併記されていることが多い。しかし、その近似が許容できる範囲のものかどうかはシミュレーションを行わなければ分からない。そこで、この方法の妥当性を調べるシミュレーションを行う。また、より信頼できる方法を開発する。

成果の内容・特徴

F検定を用いる方法の妥当性を調べるためのシミュレーション・データを作成するために以下の式を用いる。 x_i = 0.1 i, y_i = 2 x_i + 3 + αsin(0.05 π x_i) + e_i それぞれのデータセットは、{x_i, y_i } (1 ≦ i ≦ 200)(x_iがデータの予測変数の部分,y_iがデータの目的変数の部分)である。{ e_i } (1 ≦ i ≦ 200), N(0.0, 3.0²)(平均が0.0,分散が3.0²の正規分布)の実現値である。αの値として、0, 0.5, 1, 1.5, 2, 2.5, 3の7通りを設定し、αのそれぞれの値に対して、乱数の初期値を替えることで 1000組のデータセットを作成した。αの値が0のときのデータセットの例が図1であり、αの値が2のときのデータセットの例が図2である。
それぞれのデータセットを直線に回帰するべきかどうかを検定するためにF検定を行った。その際に求めるF値は以下のものである。ここで、RSS₁は、直線にあてはめたときの残差2乗和で、RSS₂は、ノンパラメトリック回帰(ここでは、平滑化スプライン)を用いた回帰式をあてはめたときの残差2乗和である。nはデータ数df1は、直線にあてはめたときの有効自由度なので2である、df2は、ノンパラメトリック回帰を行ったときの有効自由度(ここでは、n - trace(2H) + trace(H Ht)(nはデータ数、Hはハット行列))の近似値である。
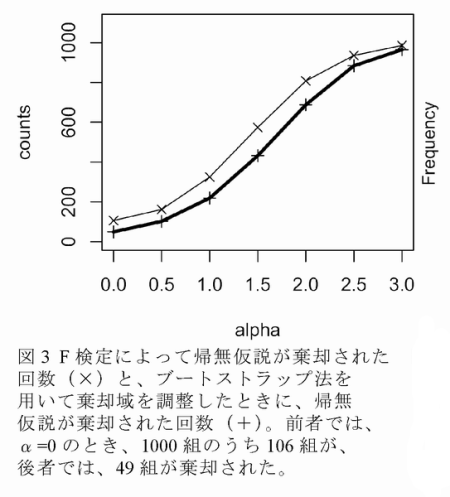
従来法(F検定をそのまま使う方法)の結果が図3の「X」である。5パーセント検定を行っているので、α=0のとき5パーセントが棄却されるべきであるのに、10パーセント程度が棄却されている。
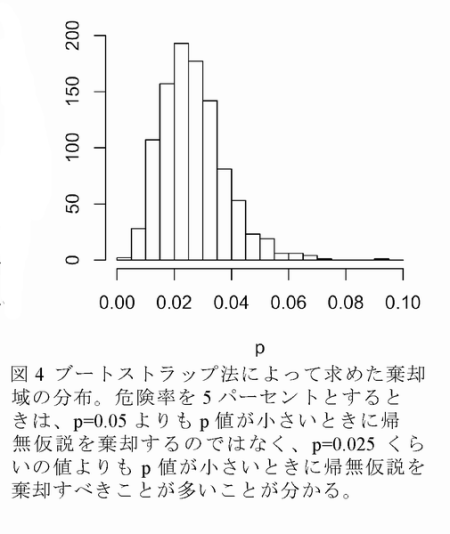
新たに考案した方法(ブートストラップ法を用いてF検定の閾値を調整する方法)の結果が図3の「+」である。5パーセント検定をほぼ実現している。αが正のとき、図2のような、直線を使って得たデータと見分けにくいデータを扱っているにもかかわらず、検出力が高い。図4に示すように、この新しい方法は棄却域を大幅に調整している。