単回帰において、最小2乗法がもたらす傾きは修正する必要がある。

要約

単回帰を行う際、最小2乗法の結果をそのまま使うと、将来のデータに対する最適な回帰式にはならない。最小2乗法で得られた単回帰式の傾きの絶対値をやや小さくする必要がある。傾きの絶対値が小さいときと、傾きの分散が大きいときに、大きな補正を行うべきである。この方法で得られた単回帰式は、予測能力の点で優れた回帰式である。

• キーワード:傾き、最尤法、単回帰、バイアス回帰、不偏性、ベイズ推定、予測誤差
• 担当:IT高度生産システム・先進的統計モデリング
• 代表連絡先:電話 029-838-8481
• 研究所名:中央農業総合研究センター・情報利用研究領域
• 分類:研究成果情報

背景・ねらい

単回帰を行う際、データの目的変数に含まれている誤差の大きさがほぼ一定で、誤差のそれぞれが独立していると考えられるとき、最小2乗法が利用されてきた。これは、ガウス・マルコフの定理が、最小2乗法が与える推定量が最良線形不偏推定量であることを保証しているためである。一方、不偏推定量とは異なる推定量を用いることで、最小2乗法より予測の点で優れた結果を与える方法として、リッジ回帰とジェームズ・スタイン推定量がある。しかし、クロスバリデーションを伴うリッジ回帰を用いると回帰係数の分散が大きくなる。また、ジェームズ・スタイン推定量は予測変数の数が3個以上の重回帰にしか利用できない。そこで、予測の観点から最小2乗法より優れていて、回帰係数の分散が小さい回帰式が得られる可能性を検討する。

成果の内容・特徴

成果の活用面・留意点

• 最小2乗法による単回帰は、農学や生物学などのデータ解析において200年くらいに渡って広く利用されてきた。従って、本手法は多くの分野のデータ解析に影響を及ぼす。
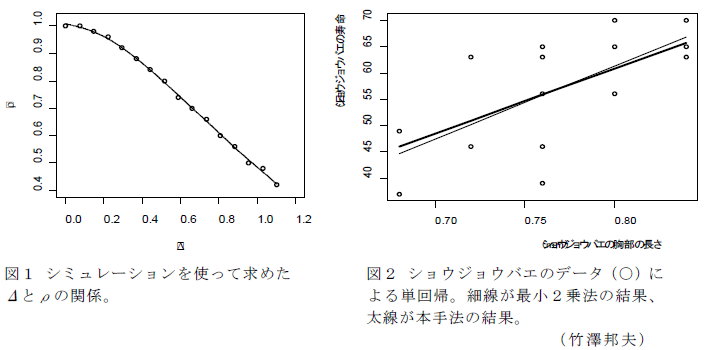
• 図1の曲線を、シミュレーションを使わずに解析的に導出することも可能かも知れないので、今後の研究の進展を待たなければならない。
• 本手法を単回帰以外の回帰に応用できる可能性もある。

具体的データ

その他

• 中課題名:業生産性向上に寄与する先進的統計モデリング手法の開発
• 中課題番号:160c0
• 予算区分:交付金
• 研究期間:2011～2012年度
• 研究担当者:竹澤邦夫
• 発表論文等:
  1)竹澤邦夫(2012)応用統計学、41(1): 39-52
  2)竹澤邦夫(2012)シミュレーションで理解する回帰分析(共立出版)