関数関係を明らかにする目的で重回帰を行うときは、GCVに替えてGCV_fを使う。

要約

重回帰を行うときの予測変数の選択には、GCV(一般化クロスバリデーション)やAIC(赤池の情報量基準)を用いるのが通例である。これらは、予測誤差を表す統計量である。しかし、関数関係の有無を明らかにするためには異なった統計量が必要になる。そこで、新しい統計量GCV_f(fはflexibleを意味する)を提案する。

• キーワード:危険率、GCV_f、重回帰、モデル選択、予測誤差
• 担当:IT高度生産システム・先進的統計モデリング
• 代表連絡先:電話 029-838-8481
• 研究所名:中央農業総合研究センター・情報利用研究領域
• 分類:研究成果情報

背景・ねらい

重回帰を行う際には、GCVやAICを用いて予測変数を選択するのが普通である。しかし、これらの統計量は重回帰式の予測誤差を表すものなので、目的変数との間に線形の関数関係が存在する予測変数を選択しているとは限らない。そこで、目的変数との間に線形の関数関係が存在しないにもかかわらず、予測変数が選択されてしまう確率を、例えば10パーセントにする方法が必要になる。

成果の内容・特徴

成果の活用面・留意点

• 農学や生物学における回帰の主な目的は、関数関係の発見である。従って、GCVやAICに替えて、GCV_fを用いるべき場面は多い。
• この方法は従来の方法より予測変数の採用に関する危険率を小さくするものなので、検出力は小さくなる。つまり、採用するべき予測変数を採用しない確率が高くなる。
• 40年位に渡って、回帰分析には検定と予測の2つの分野があった。今後は、知識発見という3つめの分野が重要な役割を果たす。GCV_fはその先駆となる。

具体的データ

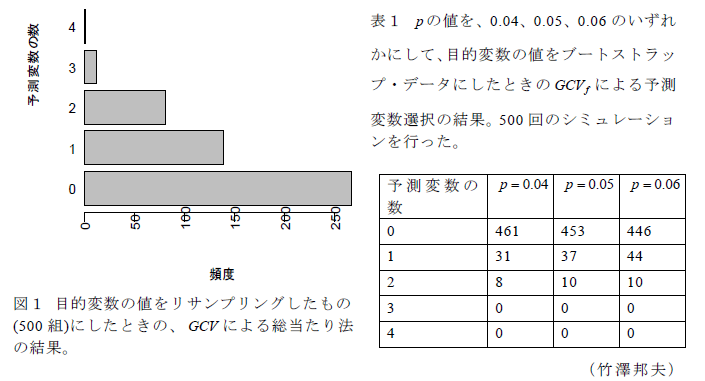
その他

• 中課題名:農業生産性向上に寄与する先進的統計モデリング手法の開発
• 中課題番号:160c0
• 予算区分:交付金
• 研究期間:2011～2012年度
• 研究担当者:竹澤邦夫
• 発表論文等:
  1)竹澤邦夫(2012)応用統計学、41(2) 97-111.
  2)Takezawa K.(2012) Open Journal of Statistics. 2(4):401-407.
  3)竹澤邦夫(2012) シミュレーションで理解する回帰分析(共立出版)