知識獲得を目的とする樹形モデルの最適化には、予測誤差ではなく純度を使う。

要約

樹形モデルの分岐ルールの数を最適化するために予測誤差を使うことが多い。しかし、分岐ルールを知識と見なすには、分岐ルールの中の知識と見なせるものの割合(純度)を制御する必要がある。これにより、直感に沿った樹形モデルが得られる可能性が高くなる。

• キーワード:樹形モデル、純度、分岐ルール、モデル選択、予測誤差
• 担当:IT高度生産システム・先進的統計モデリング
• 代表連絡先:電話 029-838-8481
• 研究所名:中央農業総合研究センター・情報利用研究領域
• 分類:研究成果情報

背景・ねらい

樹形モデルはデータマイニングの代表的な手法である。農業情報の解析やモデル化においても広く利用されている。優れた樹形モデルを得るためには、分岐ルールの数の最適化が必要になる。分岐ルールの数を決定するたに予測誤差が主に使われてきた。しかし、分岐ルールのそれぞれをデータに含まれている知識と見なすためには、分岐ルールの中にデータに含まれる知識と見なせるものがどのくらいあるかが重要である。そこで、分岐ルールの中の知識として妥当なものの割合を純度と定義して、純度を用いて分岐ルールの数を最適化する。

成果の内容・特徴

• 予測変数が4つあり、x₁:1人あたりの犯罪率、x₂: 小売店以外の事業所の面積の割合、x₃:1戸あたりの部屋数の平均、x₄:教員1人あたりの生徒の数 である。目的変数は、y: 持ち主が住んでいる家の価格の中央値(単位は千ドル)を対数変換したもの、である。データ数は400個。
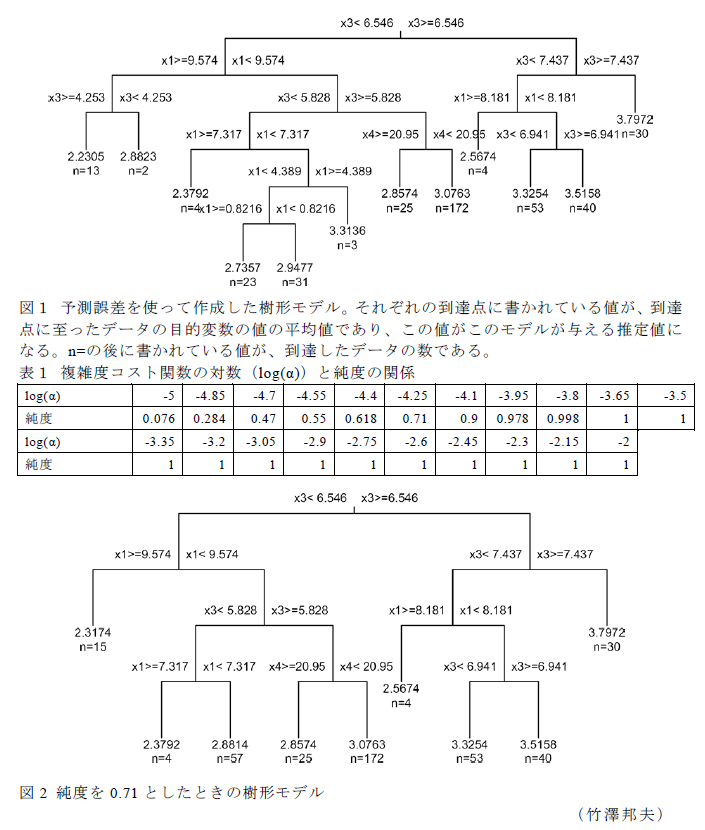
• このデータを用いて、予測誤差を使って作成した樹形モデルが図1である。複雑度コスト測度(分岐ルールの数を与える定数、α)の対数は-4.828、分岐ルールの数は11個である。左端の分岐ルールは、x₃(部屋の数)が小さい家の価格が高くなることを示している。これは、この樹形モデルにおけるx₃に関する他の分岐ルールに対立し、常識にも反する。「逆転現象」と呼ぶべきものである。x₁に関して不合理な分岐ルールが見られる。
• x₅をx₁の値を、重複を許してランダムにサンプリングしたもの、x₆をx₂の値を、重複を許してランダムにサンプリングしたもの、x₇をx₃の値を、重複を許してランダムにサンプリングしたもの、x₈をx₄の値を、重複を許してランダムにサンプリングしたもの、とする。乱数の初期値を替えて、この形式のデータを500組作成する。
• 500組のそれぞれを使い、αとして様々な値を用いて樹形モデルを作成する。
• x₅からx₈はランダムな値なので、樹形モデルの中の分岐ルールで用いられるべきではない。そこで、x₅からx₈が用いられていない樹形モデルの割合を純度と定義する。すると、4の結果から、複雑度コスト関数の対数(log(α))と純度の関係が得られる(表1)。
• 純度を0.71にしたときの樹形モデルが図2である。分岐ルールの数は8個である。2で指摘した不合理な分岐ルールがなくなっている。純度を0.978にすると、分岐ルールの数が6個になる。

成果の活用面・留意点

• 表1では純度が1.0のものがあるけれども、不合理な分岐ルールが現れる可能性をゼロにすることはできない。
• 適切な純度の値は樹形モデルを利用する目的に依存する。

具体的データ

その他

• 中課題名:農業生産性向上に寄与する先進的統計モデリング手法の開発
• 中課題番号:160c0
• 予算区分:交付金
• 研究期間:2011～2012年度
• 研究担当者:竹澤邦夫
• 発表論文等:K. Takezawa(2012) Open Journal of Statistics 2(5): 478-483