土壌物理性の不均一度のスケール依存性評価のための間隙構造モデル

※アーカイブの成果情報は、発表されてから年数が経っており、情報が古くなっております。
同一分野の研究については、なるべく新しい情報を検索ください。

要約

土壌の間隙を粗間隙と土壌マトリクスの2領域に区分し、土壌物理性をこれらの領域で定義された確率変数の関数として表すことより、土壌物理性の統計的な分布とサンプルの大きさとの関係を理論的に検討しうる間隙構造モデルを開発した。

  • 担当:農業工学研究所・農地整備部・水田整備研究室
  • 代表連絡先:0298-38-7555
  • 部会名:農業工学
  • 専門:農地整備
  • 対象:現象解析技術
  • 分類:研究

背景

近年、水田においては直播栽培のための土壌・水管理技術の確立などにあたり、土壌中の物質量の推定や移動現象の予測精度の向上のため、飽和透水係数や乾燥密度などの土壌物理性の不均一性の評価手法の確立が要請されている。サンプリングに基づいて不均一性を統計的に評価する場合、サンプルの数、空間的配置、大きさの設定が必要である。しかしながら、土壌物理性の統計的な分布はサンプルの大きさ(スケール)に依存することが経験的に知られており、同一の土壌において土壌物理性の平均、分散に関して異なった結果が得られるという問題があった。そこで、ここでは、土壌物理性の値と密接に関連する土壌の間隙分布に着目し、水田の耕盤層を対象として土壌物理性の統計的な分布とサンプルの大きさとの関係を理論的に取り扱うことが可能な間隙構造モデルの開発を行った。

成果の内容・特徴

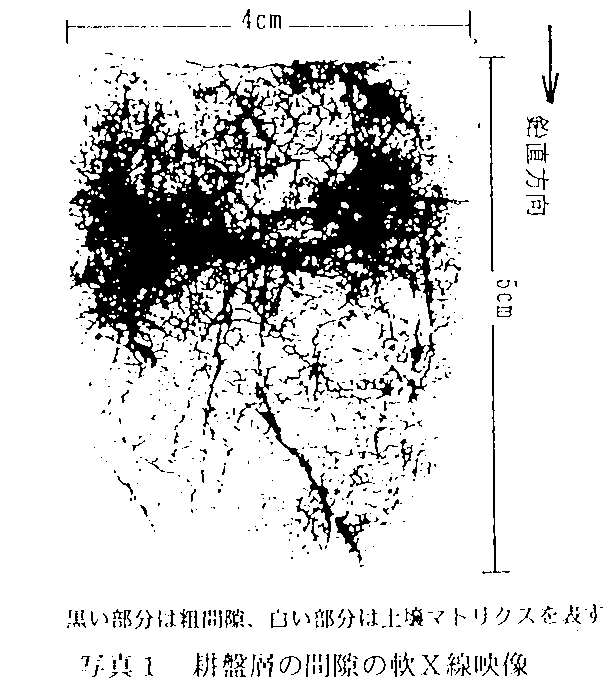
  • 間隙構造モデル:耕盤層の間隙構造(写真1)を毛管状の粗間隙と土壌マトリクス(微細な間隙と固相から成る土壌のカベ状の部分)の2領域に区分し(図1)、確率論により粗間隙の単位面積当たりの本数をポアソン確率変数、既往の知見により土壌マトリクス中の間隙率を正規確率変数として定義した。
  • 土壌物理性の確率変数としての表示:土壌物理性には、飽和透水係数などその値が粗間隙に支配される項目と、乾燥密度など粗間隙と土壌マトリクスの間隙の両方に支配される項目とがある。そこで、1:)で定義した粗間隙の本数と土壌マトリクスの間隙率の2つの確率変数を用いて、土壌物理性をサンプルの大きさを変数として含むこれらの関数として表した(図2)。
  • 以上のモデルにより、粗間隙の本数及び土壌マトリクスを表す確率変数の分布の母数とこれらの確率変数間の相関係数を与えることにより、任意のサンプルの大きさにおける土壌物理性の平均、分散等の期待値及び分布形を予測することができる。分布形の予測例を表1に示す。表1は断面積が増えると分布が対数正規から正規形へ移行することを示す。

成果の活用面・留意点

  • 適用範囲:本モデルは、水田の耕盤層など、粗間隙が鉛直方向に卓越した管状孔隙から構成されている土層に適用することが可能である。
  • 活用面:本モデルを用いて、目的とする推定精度を満足する土壌物理性の平均を得るために必要なサンプルの大きさを検討することができる。
  • 留意点:土壌物理性の分布とサンプルの大きさとの関係の理論的検討に必要な確率変数の分布の母数、及びこれらの間の相関係数は、サンプリングによって推定することが必要である。

具体的データ

写真1 耕盤層の間隙の軟X線映像
図1 耕盤層の間隙モデル
図2 土壌物理性の確率変数表示
表1 飽和透水係数の分布形の検討例

その他

  • 研究課題名:土壌条件の解明による作土層水分制御技術の高度化、作土層の迅速・均一な水分制御システムの開発
  • 予算区分:総合的開発研究(軽労化農業)
  • 研究期間:平6～10
  • 研究担当者:原口暢朗、安中武幸
  • 発表論文等:1)岡部和典、原口暢朗、安中武幸:飽和透水係数および乾燥密度の面的な平均値推定のためのサンプリング要素の設定条件に関する事例的検討、農土論集,184,pp.175～183,1996
    2)原口暢朗・安中武幸:土壌間隙構造モデルに基づく飽和透水係数の不均一性に関する確率論的考察、農土論集190,pp.27～33,1997
    3)N.Haraguchi:A Stochastic Study on the Heterogeneity of Saturated Hydraulic Conductivity,Agronomy Abstracts of 89th ASA Annual Meeting,pp.162,1997