フェルミ・ディラック分布関数を用いた非線形回帰による気温上昇特性の解析
※アーカイブの成果情報は、発表されてから年数が経っており、情報が古くなっております。
同一分野の研究については、なるべく新しい情報を検索ください。
要約
フェルミ・ディラック分布関数を用いた非線形回帰によって、平均化された時別気温を2つの係数のみで近似し、気温上昇の特性を簡易に比較できる手法。この手法により、様々なAMeDAS観測点における気温上昇特性の違いを解析できる。
- キーワード:非線形回帰、フェルミ・ディラック分布関数、AMeDAS気温、気温上昇特性
- 担当:近中四農研・暖地温暖化研究近中四サブチーム
- 連絡先:電話084-923-4100
- 区分:共通基盤・農業気象
- 分類:研究・参考
背景・ねらい
AMeDAS観測点は、平野部や海岸、山間部等、多様な地理条件下に分布しているため、平均気温、最高・最低気温、日較差等も多 様な値を示す。また、気温の変化特性、特に上昇特性にも地域固有の特徴が認められる。しかしながら、そうした上昇特性の地域差を、シンプルに整理して比較 する手法はなかった。そこで、最低気温から最高気温までの時間帯の気温値を変換して非線形近似することにより、AMeDAS観測点における気温上昇特性を 簡易に抽出する手法を開発する。
成果の内容・特徴
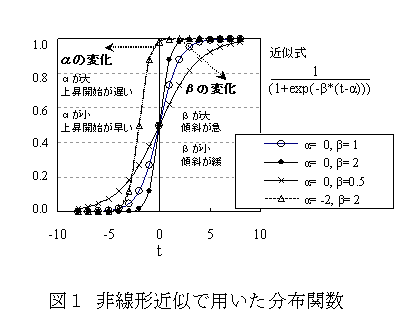
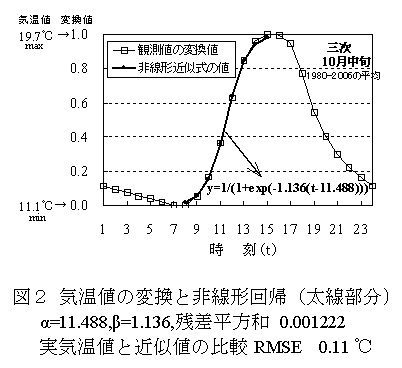
- 平均化された最低気温形成時~最高気温形成時の気温上昇曲線(時別値)は、フェルミ・ディラック分布関数を用いることによ り、2つの係数(α、β)のみで近似できる(αの次元は時間で、βは無次元)。この回帰式で、係数αの値が大きいことは、気温上昇に時間遅れが存在するこ とを意味する。一方、係数βについては、気温が上昇する時間帯の中頃に急上昇する場合に大きく、早朝から持続的に上昇する場合に小さくなる(図1、2)。
- 70日以上の時別データ(月別では約3年分、旬別では7年分)を使って平均化すれば、αの変動幅は0.5時間以内、βの変動幅は0.2以内に収束し、地点間の気温上昇特性の違いを判別できる。
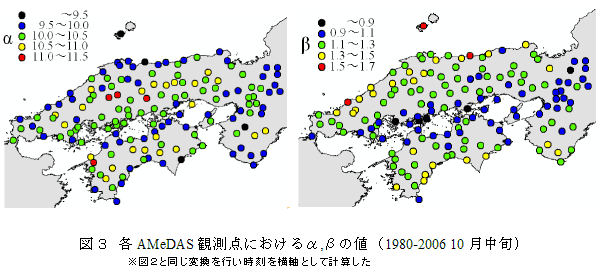
- 近畿・中国・四国地域に位置するAMeDAS観測点(151地点)について、10月中旬のα,βの値を示す(図3)。中山間地、特に霧がよく発生する観測点ではαの値が大きく、海に近い観測点では小さい傾向にある。また、βの値は日本海や太平洋の沿岸で大きく、瀬戸内海沿岸では小さい。
成果の活用面・留意点
- 本研究の解析では、フェルミ・ディラック分布関数をExcelのSolver機能を利用して、最小自乗法により決定した。
- 非線形回帰の誤差の大きさを示す残差平方和の値は、151地点のうち最小値が0.0006(美山)、最大値が0.02(下市)で、151観測点の平均は0.0065である。実際の気温値でのRMSEは0.06℃(美山)、0.23℃(下市)である。
具体的データ
その他
- 研究課題名:暖地・温暖地における気候温暖化等環境変動に対応した農業生産管理技術の開発
- 課題ID:215-a
- 予算区分:基盤
- 研究期間:2006~2007年度
- 研究担当者:佐藤恵一
